3.1 Twee probabilistische bits ‣ Quest 3: Magie van verstrengeling ‣ De Quantum Quest‣ Quest 3: Magie van verstrengeling ‣ De Quantum Quest

Als je twee muntjes op een tafel hebt liggen, dan zijn er vier mogelijke configuraties:

Deze komen overeen met de vier mogelijke bitstrings¹²¹² 12 Met een ‘string’ bedoelen we een ‘reeks van tekens’, of in dit geval een reeks van bit-waarden. Dit is een handige notatie om aan te geven hoe je muntjes liggen, vooral als we naar meerdere muntjes kijken.: 00, 01, 10, 11.

Als je twee probabilistische bits hebt, wordt hun toestand beschreven door een kansverdeling over deze vier mogelijke deterministische toestanden. Met andere woorden, hun toestand wordt beschreven door vier getallen $p_{00},p_{01},p_{10},p_{11}\geq 0$ , waarbij $p_{00}+p_{01}+p_{10}+p_{11}=1$ . Net als in het geval van een enkele bit kunnen we dit opschrijven als een vector

\begin{pmatrix}p_{00}\\ p_{01}\\ p_{10}\\ p_{11}\end{pmatrix}.

(3.1)

Hoewel deze weergave volledig correct is, is het nogal onhandig omdat het moeilijk kan zijn om bij te houden welke waarschijnlijkheid hoort bij welke bitconfiguratie (is het eerst $p_{10}$ of $p_{01}$ ?!), en het wordt alleen maar ingewikkelder als we meer dan twee bits hebben. Het is veel handiger om een notatie te gebruiken waarmee we direct kunnen bijhouden welke waarschijnlijkheden zijn toegewezen aan bepaalde bitstrings. We breiden daarom de notatie uit die we gebruikten in Vgl. 1.7 voor een enkele probabilistische bit en schrijven de bovenstaande twee-bits-toestand als volgt:

p_{00}[00]+p_{01}[01]+p_{10}[10]+p_{11}[11].

(3.2)

Als je wilt, kun je deze notatie altijd omzetten naar de 4-vector notatie in Vgl. 3.1 door gebruik te maken van de volgende uitbreiding van Vgl. 1.6:

[00]=\begin{pmatrix}1\\ 0\\ 0\\ 0\end{pmatrix},\qquad[01]=\begin{pmatrix}0\\ 1\\ 0\\ 0\end{pmatrix},\qquad[10]=\begin{pmatrix}0\\ 0\\ 1\\ 0\end{pmatrix},\qquad[11]=\begin{pmatrix}0\\ 0\\ 0\\ 1\end{pmatrix}.

(3.3)

Een voordeel van deze notatie in het geval van meerdere bits is dat we elementen die nul zijn gewoon weg kunnen laten. We kunnen bijvoorbeeld gewoon schrijven

\displaystyle\frac{1}{2}[00]+\frac{1}{2}[11]

in plaats van het veel onhandigere

\displaystyle\frac{1}{2}[00]+0\,[01]+0\,[10]+\frac{1}{2}[11].

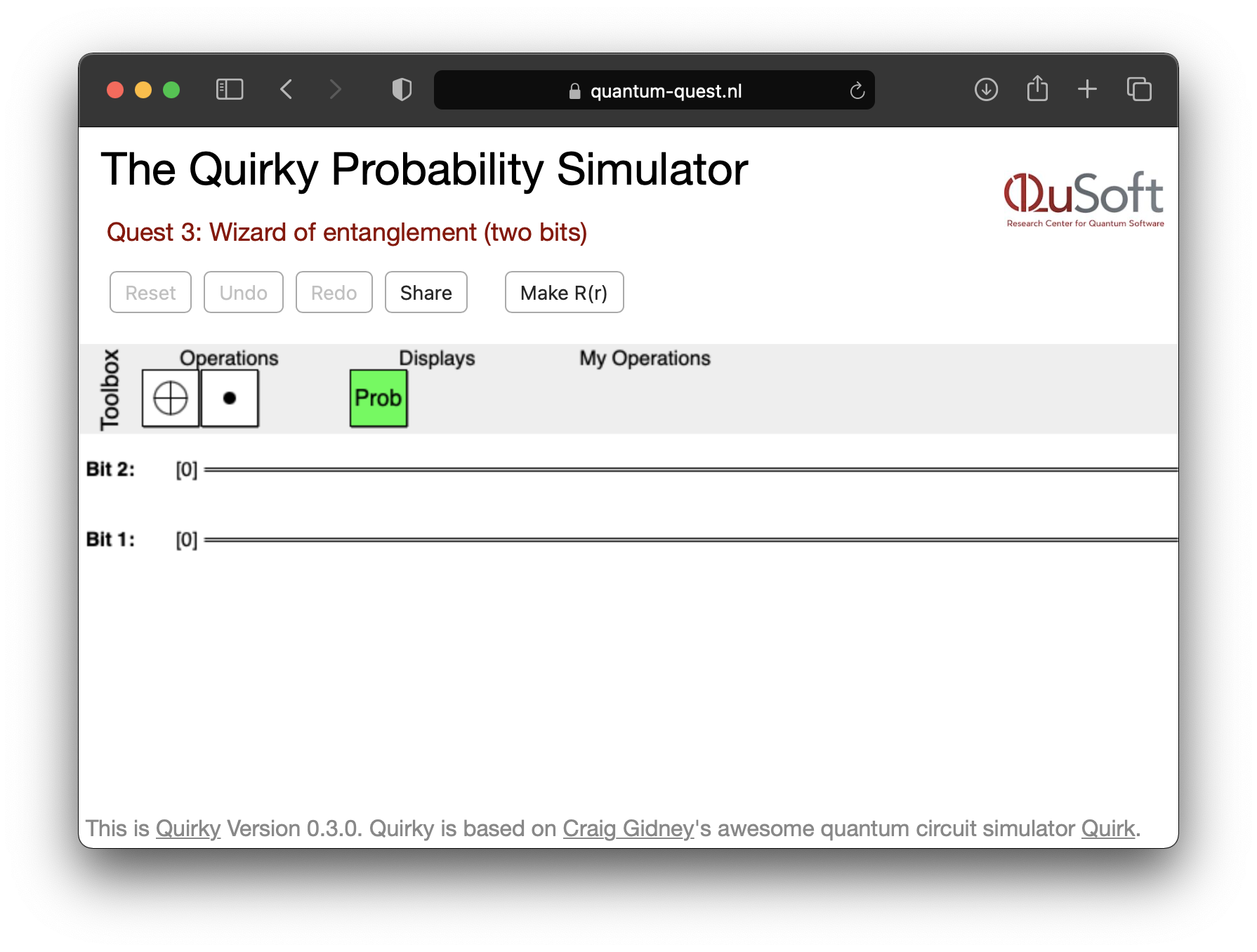
Met deze notatie is het ook veel eenvoudiger om metingen en bewerkingen op meerdere probabilistische bits te beschrijven. We kunnen het gedrag van twee probabilistische bits onderzoeken met Quirky, dat sinds vorige week weer nieuwe krachten heeft gekregen. Ga om te beginnen naar:

https://www.quantum-quest.org/quirky

en klik op ’Quest 3’ en selecteer ’Two Bits’. Je webbrowser zal eruit zien als Fig. 3.1. Merk op dat we nu twee draden hebben, die overeenkomen met twee bits, die zijn ingesteld in de toestand $[00]$ . Het is misschien verrassend dat het eerste bit overeenkomt met de onderste draad en het tweede bit met de bovenste draad. Daarnaast is er een nieuwe vakje: $\bullet$ (maar het mysterievakje is verdwenen). De betekenis van dit vakje bespreken we later in dit hoofdstuk.