3.1.4 De toestand van het andere bit

Na de meting zit het bit dat gemeten is in een deterministische toestand die hoort bij de uitkomst van de meting (net als bij het meten van een enkele bit – zie Vgl. 1.32). Maar hoe zit het met het andere bit dat niet gemeten is? De toestand na de meting zal in het algemeen niet deterministisch zijn. Bijvoorbeeld, als de begintoestand van de twee probabilistische bits

\frac{1}{2}[10]+\frac{1}{2}[11]

(3.15)

is en het eerste bit wordt gemeten, is de kans op het waarnemen van uitkomst $1$ gelijk aan $1/2+1/2=1$ . Met andere woorden, het eerste bit in Vgl. 3.15 is deterministisch en de twee waarschijnlijkheden beschrijven eigenlijk alleen het tweede bit. Je kunt deze toestand dus beschouwen als het resultaat van het samenvoegen van twee afzonderlijke probabilistische bits: $[1]$ en $\frac{1}{2}[0]+\frac{1}{2}[1]$ (we zullen meer vertellen over het combineren van twee probabilistische bits in Paragraaf 3.1.7). Het is dus logisch dat de toestand van het tweede bit na de meting uniform random is, namelijk

\frac{1}{2}[0]+\frac{1}{2}[1].

In het algemeen kunnen we beginnen met twee probabilistische bits in een arbitraire toestand

\displaystyle p_{00}[00]+p_{01}[01]+p_{10}[10]+p_{11}[11]

(3.16)

en we meten het eerste bit. De toestand van het overgebleven bit hangt in het algemeen af van de uitkomst van de meting. Als de uitkomst bijvoorbeeld $1$ was, verzamelen we om de toestand van het tweede bit te vinden eerst alle termen van Vgl. 3.16 waarbij het eerste bit de waarde $1$ heeft:

p_{10}[10]+p_{11}[11].

Dan negeren we het eerste bit omdat we al weten dat die waarde $1$ is:

p_{10}[0]+p_{11}[1].

Als laatste, omdat deze twee kansen waarschijnlijk niet samen één zijn, delen we ze door hun som $p_{10}+p_{11}$ :

\frac{p_{10}}{p_{10}+p_{11}}[0]+\frac{p_{11}}{p_{10}+p_{11}}[1].

(3.17)

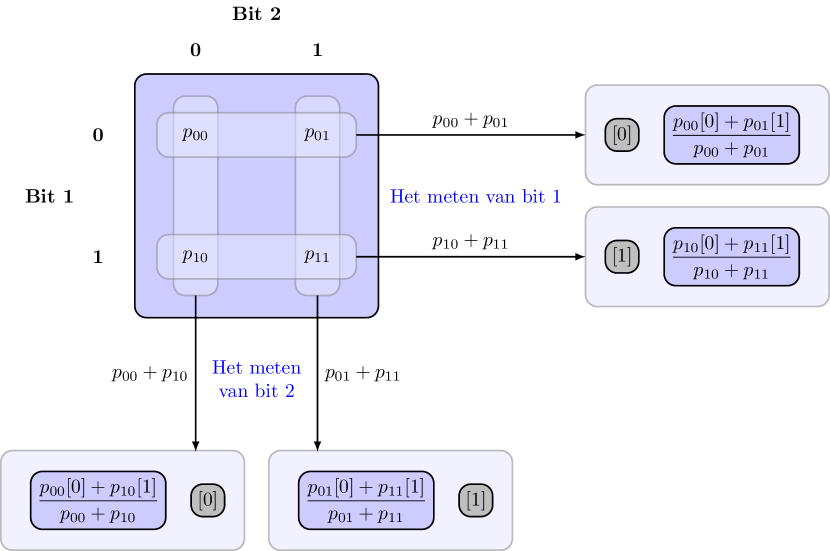
Dit is de kansverdeling voor het tweede bit wanneer het eerste bit gemeten wordt en uitkomst $1$ oplevert (zie de rechterkant van Fig. 3.3). De overige gevallen worden ook samengevat in Fig. 3.3.

Refer to caption — Figuur 3.3: De mogelijke uitkomsten wanneer we slechts een van de twee probabilistische bits meten. Voor elke mogelijke uitkomst geven we de waarschijnlijkheid (zwarte pijl) en de overgebleven toestand. Na de meting wordt het gemeten bit deterministisch (grijs) terwijl het andere bit probabilistisch blijft (lichtblauw).

Om te controleren of deze regels logisch zijn, kunnen we nagaan of het meten van het eerste bit en vervolgens het tweede bit tot dezelfde waarschijnlijkheden leidt als het direct meten van beide bits. De kans dat je bijvoorbeeld $1$ krijgt van het eerste bit en $0$ van het tweede bit zou gewoon $p_{10}$ moeten zijn. Volgens Vgl. 3.14, krijgen we uit het eerste bit de uitkomst $1$ met waarschijnlijkheid $p_{10}+p_{11}$ en, gegeven deze uitkomst, stelt Vgl. 3.17 dat het tweede bit $0$ geeft met waarschijnlijkheid $p_{10}/(p_{10}+p_{11})$ . Dus de totale kans om eerst $1$ uit het eerste bit te krijgen en dan $0$ uit het tweede bit is

\displaystyle\left(p_{10}+p_{11}\right)\times\frac{p_{10}}{p_{10}+p_{11}}=p_{1% 0},

wat precies is wat we willen volgens Vgl. 3.4. De andere gevallen kunnen op dezelfde manier worden gecontroleerd.

Oefenopgave 3.2 (Alice’ muntje raden).

Het probleem: Alice heeft drie muntjes die we $u$ , $q$ en $r$ noemen, met de volgende kansverdelingen:

\displaystyle u=\begin{pmatrix}1/2\\ 1/2\end{pmatrix},

\displaystyle q=\begin{pmatrix}3/4\\ 1/4\end{pmatrix},

\displaystyle r=\begin{pmatrix}1/3\\ 2/3\end{pmatrix}.

Alice gooit de muntjes op volgens het volgende stappenplan:

1.

Ze gooit muntje $u$ op.
2.
Afhankelijk van de uitkomst gooit ze een van de andere twee muntjes op:
1. (0)
  
  als $u$ op $0$ uitkwam, gooit ze $q$ op;
2. (1)
  
  als $u$ op $1$ uitkwam, gooit ze $r$ op.
3.

Alice vertelt haar vriend Bob wat de uitkomst ( $0$ of $1$ ) van de laaste worp is (maar ze vertelt niet of deze uitkomst van muntje $q$ of $r$ komt).

In deze situatie zijn er twee probabilistische bits: Alice’ eerste worp en Alice’ tweede worp (die precies hetzelfde is als Bob’s probabilistische bit).

Vragen:

1.

Wat is de kansverdeling van Alice’ twee worpen?
2.

Wat is de kansverdeling als Bob zijn probabilistische bit meet?
3.

Als gegeven is dat Bob zijn bit meet en uitkomst $0$ krijgt, is het dan waarschijnlijker dat Alice’ eerste munt op $0$ of $1$ was uitgekomen? Hoe zit het als zijn uitkomst $1$ is?

Solution.

1.

We duiden de kansverdelingen van Alice‘ twee worpen aan met $p$ . We gebruiken Fig. 3.3 om de kansen te berekenen. We weten dat de eerste munt van Alice verdeeld is volgens $u$ , wat betekent dat als we het eerste bit meten, we beide uitkomsten krijgen met kans $1/2$ :

$\displaystyle p_{00}+p_{01}=\frac{1}{2},\quad p_{10}+p_{11}=\frac{1}{2}.$

Vervolgens weten we dat als het opgooien van het eerste muntje uitkomst $0$ gaf, de toestand van het tweede bit beschreven moet worden door het muntje $q$ . Er moet dus gelden dat

$\displaystyle\frac{p_{00}[0]+p_{01}[1]}{p_{00}+p_{01}}=\frac{3}{4}[0]+\frac{1}% {4}[1],$

waaruit we afleiden dat $p_{00}=\frac{3}{8}$ en $p_{01}=\frac{1}{8}$ . Als de eerste worp uitkomst $1$ gaf, dan wordt de toestand van het tweede bit beschreven door munt $r$ , dus

$\displaystyle\frac{p_{10}[0]+p_{11}[1]}{p_{00}+p_{01}}=\frac{1}{3}[0]+\frac{2}% {3}[1],$

dus $p_{10}=\frac{1}{6}$ en $p_{11}=\frac{2}{6}$ . Samen geeft dit

$\displaystyle p=\frac{3}{8}[00]+\frac{1}{8}[01]+\frac{1}{6}[10]+\frac{2}{6}[11],$
2.

De waarde van Bob’s bit is hetzelfde als de uitkomst van Alice’ tweede muntworp, dus we volgen gewoon Fig. 3.3 om de waarschijnlijkheid van de uitkomsten te berekenen bij het meten van het tweede bit. De kans dat de uitkomst van Bob $0$ is, is dus

$\displaystyle p_{00}+p_{10}=\frac{3}{8}+\frac{1}{6}=\frac{13}{24}$

en de kans dat zijn uitkomst $1$ is, is $1-\frac{13}{24}=\frac{11}{24}$ . We kunnen dit beschrijven als de kansverdeling

$\displaystyle\frac{13}{24}[0]+\frac{11}{24}[1].$
3.

Ook hier gebruiken we weer Fig. 3.3. Als het tweede bit gemeten wordt en het resultaat is uitkomst $0$ dan wordt de toestand van het eerste bit gegeven door

$\displaystyle\frac{p_{00}[0]+p_{10}[1]}{p_{00}+p_{10}}=\frac{9}{13}[0]+\frac{4% }{13}[1].$

Het is dus waarschijnlijker dat Alice’ eerste muntje op $0$ was geland.

Net zo geldt dat als het resultaat van het meten van het tweede bit $1$ is, de toestand van het eerste bit wordt beschreven door

$\displaystyle\frac{p_{01}[0]+p_{11}[1]}{p_{01}+p_{11}}=\frac{3}{11}[0]+\frac{8% }{11}[1].$

In dit geval is het waarschijnlijker dat Alice’ eerste munt op $1$ was geland.