3.1.3 Het meten van één bit

Als je twee probabilistische bits hebt en je meet er maar één, wat zijn dan de kansen dat je elk van de twee mogelijke uitkomsten krijgt? Onze notatie is bijzonder geschikt om dit uit te zoeken. We nemen weer een algemene probabilistische twee-bits toestand

Als je de kans op uitkomst $0$ wilt vinden bij het meten van een bit, tel je gewoon de kansen op van alle termen waarbij het bit dat je meet in de gewenste toestand $0$ zit. Hetzelfde geldt voor de uitkomst $1$.

De kans om uitkomst $1$ te krijgen als je eerste bit meet, is bijvoorbeeld

wat overeenkomt met de waarschijnlijkheden van Vgl. 3.4 die leiden tot $[10]$ en $[11]$, de twee bitstrings die beginnen met $1$. Op dezelfde manier is de kans op het waarnemen van uitkomst $0$ bij het meten van de tweede bit

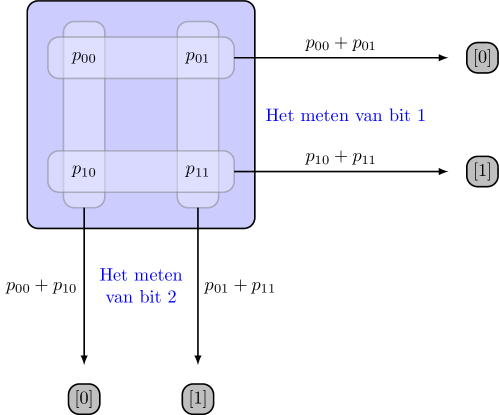
wat overeenkomt met de kansen die leiden tot de twee bitstrings die eindigen op nul, $[00]$ en $[10]$. Een makkelijke manier om dit te berekenen is door de vier kansen in een $2\times 2$ vierkant te zetten, zoals in Fig. 3.2.

We kunnen ook Quirky gebruiken om de waarschijnlijkheden te laten zien als je een enkele bit meet. Je hoeft alleen maar het formaat van de Probability Display aan te passen zodat het alleen op een enkele draad staat, zoals in het volgende voorbeeld:

Je kan zelfs tegelijkertijd meten wat de waarschijnlijkheden van uitkomsten zijn als je beide bits los van elkaar meet.

Merk op dat dit resultaat erg logisch is. Omdat de twee bits nooit “gecorreleerd” zijn, dus ze hebben niet met elkaar kunnen communiceren, is het duidelijk dat het eerste bit in toestand $\frac{1}{3}[0]+\frac{2}{3}[1]$ moet zitten en het tweede bit in toestand $[1]$.