3.1 Zwei probabilistische Bits ‣ Quest 3: Verzaubernde Verschränkungen ‣ Der Quantum Quest‣ Quest 3: Verzaubernde Verschränkungen ‣ Der Quantum Quest

Zwei nebeneinander liegende Münzen können sich in folgenden vier möglichen Zuständen befinden:

Diese entsprechen den vier möglichen Bitstrings¹²¹² 12 Mit einem ‘String’ bezeichnen wir eine Zeichenkette, in diesem Fall bestehend aus Bitwerten. Wir werden mehrere Münzen oder Qubits hauptsächlich durch solche Strings darstellen. :00, 01, 10, 11.

Der Zustand eines Paares von probabilistischen Bits ist durch die Wahrscheinlichkeitsverteilung über diese vier deterministische Zustände gegeben. Mit anderen Worten, der Zustand wird durch die vier Zahlen $p_{00},p_{01},p_{10},p_{11}\geq 0$ definiert, wobei $p_{00}+p_{01}+p_{10}+p_{11}=1$ . Genau wie im Falle eines einzelnen Bits können wir diesen Zustand in Vektorschreibweise so schreiben:

\begin{pmatrix}p_{00}\\ p_{01}\\ p_{10}\\ p_{11}\end{pmatrix}.

(3.1)

Diese Darstellung ist zwar akkurat, kann aber schnell verwirrend werden, weil man aufpassen muss welche Wahrscheinlichkeit wo steht (kommt $p_{10}$ zuerst oder doch $p_{01}$ ?!) und es wird nur komplizierter, je mehr Bits man hat. Viel einfacher ist es, eine Notation zu verwenden, die die Wahrscheinlichkeiten direkt den entsprechenden Bitstrings zuweist. Dafür erweitern wir die Schreibweise aus Gl. 1.7 von einem probabilistischen Bit auf zwei und beschreiben den obigen Zustand so:

p_{00}[00]+p_{01}[01]+p_{10}[10]+p_{11}[11].

(3.2)

Wenn du möchtest, kannst du diese Gleichung mit den folgenden verallgemeinerungen von Gl. 1.6 auf Gl. 3.1 zurückführen:

[00]=\begin{pmatrix}1\\ 0\\ 0\\ 0\end{pmatrix},\qquad[01]=\begin{pmatrix}0\\ 1\\ 0\\ 0\end{pmatrix},\qquad[10]=\begin{pmatrix}0\\ 0\\ 1\\ 0\end{pmatrix},\qquad[11]=\begin{pmatrix}0\\ 0\\ 0\\ 1\end{pmatrix}.

(3.3)

Ein Vorteil dieser Notation ist, dass wir im Falle von mehreren Bits Einträge die 0 sind einfach ignorieren können. So können wir zum Beispiel schreiben

\displaystyle\frac{1}{2}[00]+\frac{1}{2}[11]

anstelle von der klobigeren Notation

\displaystyle\frac{1}{2}[00]+0\,[01]+0\,[10]+\frac{1}{2}[11].

Mit dieser Notation ist es außerdem viel einfacher Messungen und Operationen auf vielen probabilistischen Bits darzustellen. Mit Quirky können wir ein bisschen mit zwei probabilistischen Bits herumspielen, denn das Tool hat wieder neue Fähigkeiten bekommen. Gehe zunächst zu

https://www.quantum-quest.org/quirky

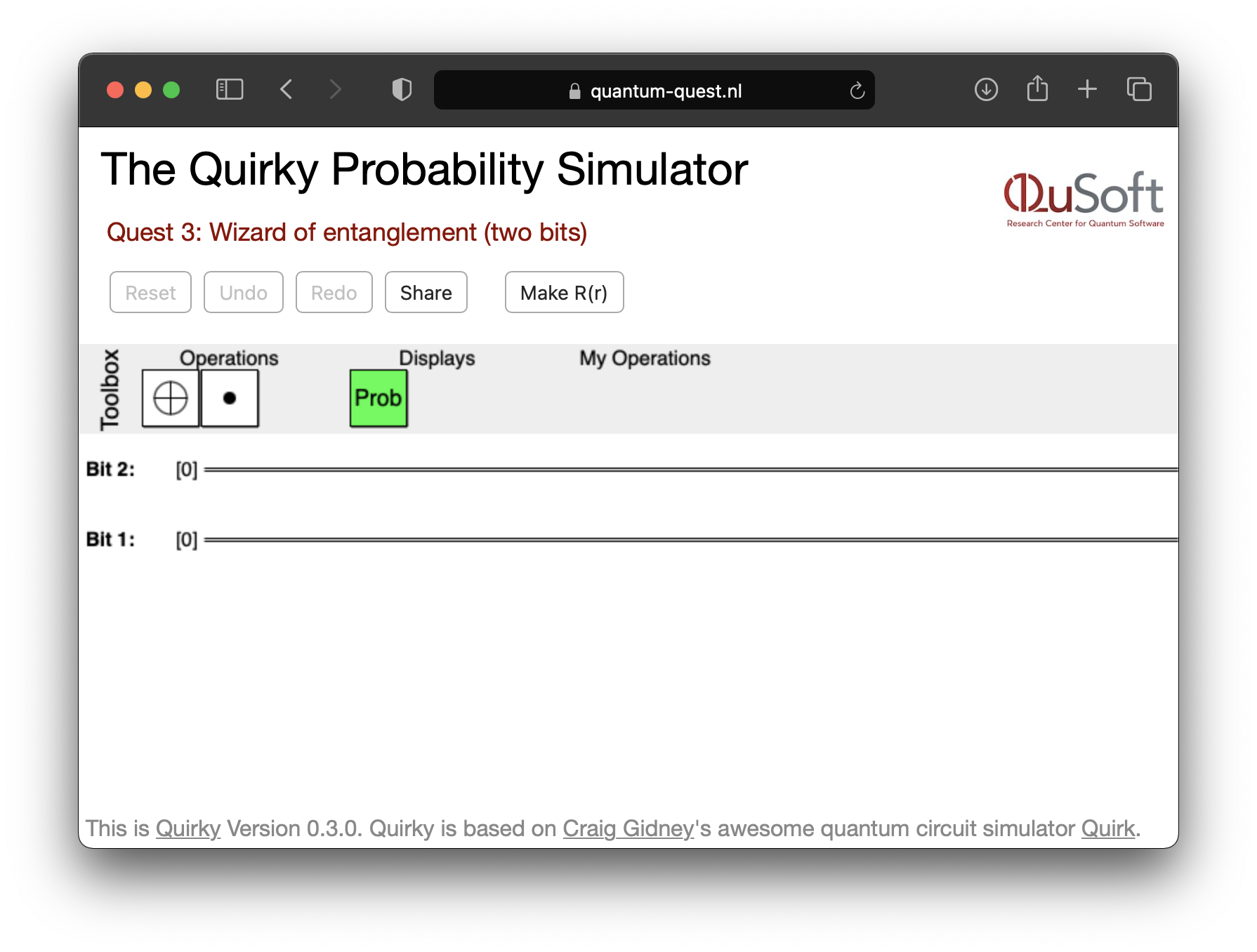
und klicke auf “Quest 3” und wähle “Two Bits” aus. Quirky sollte dann in etwa wie in Abb. 3.1 aussehen. Wie du siehst gibt es jetzt zwei Drähte, die zwei Bits entsprechen, welche im Zustand $[00]$ starten. Vielleicht überrascht es dich, dass das untere Bit das erste ist und das obere das zweite. Außerdem gibt es eine neue Operation in der Toolbox: $\bullet$ (aber dafür fehlt die Mystery-Box). Die Funktion dieser Box besprechen wir später in diesem Kapitel.