3.1.3 Nur ein Bit messen

Wenn du zwei probabilistische Bits gegeben hast und nur eines der Beiden messen willst, welche Wahrscheinlichkeiten haben dann die zwei möglichen Ergebnisse? Unsere Notation ist in diesem Fall sehr praktisch. Schauen wir uns doch nochmal den allgemeinen Zwei-Bit-Zustand an:

Um die Wahrscheinlichkeit für das Messergebnis $0$ eines Bits zu erhalten, müssen wir nur die Summe über die Wahrscheinlichkeiten aller Zustände bilden, in denen das Bit den richtigen Wert hat.

Zum Beispiel ist die Wahrscheinlichkeit, das Ergebnis $1$ beim messen des ersten Bits zu erhalten

die den Wahrscheinlichkeiten für die Zustände $[10]$ und $[11]$ aus Gl. 3.4 entsprechen, da das die beiden Bitstrings sind, die mit $1$ beginnen. Genauso ist die Wahrscheinlichkeit beim messen des zweiten Qubits $0$ zu erhalten

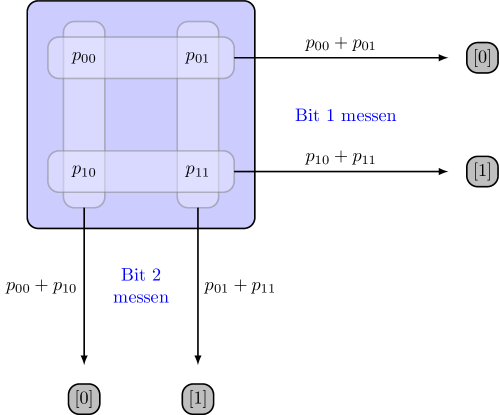
die den Wahrscheinlichkeiten für die Zustände $[00]$ und $[10]$ entsprechen, welches die Bitstrings sind, die auf $0$ enden. Wenn man die vier Wahrscheinlichkeiten in einer $2\times 2$ Form wie in Abb. 3.2 darstellt wird die Berechnung noch einfacher.

Wir können auch Quirky benutzen um die Wahrscheinlichkeiten einer Ein-Bit-Messung anzuzeigen. Verkleinere einfach die Wahrscheinlichkeitsanzeige auf das gewünschte Bit, zum Beispiel so:

Tatsächlich können wir beide Bits einzeln messen und uns beide Messergebnisse gleichzeitig anzeigen lassen:

Das Ergebnis ist sehr intuitiv. Da die beiden Bits nie “korrelieren” ist klar, dass das erste Bit im Zustand $\frac{1}{3}[0]+\frac{2}{3}[1]$ und das zweite im Zustand $[1]$ sein muss.