3.1.4 Der Zustand des anderen Bit

Nachdem ein Bit gemessen wurde, befindet sich dieses in dem entsprechenden deterministischen Zustand (genau, wie bei der Messung eines einzelnen Bits in Gl. 1.32). Aber was ist mit dem anderen Bit, das nicht gemessen wurde? Im Allgemeinen befindet sich dieses nicht in einem deterministischen Zustand. Wenn zum Beispiel im Zustand

\frac{1}{2}[10]+\frac{1}{2}[11]

(3.15)

das erste Bit gemessen wird, erhält man mit Wahrscheinlichkeit $1/2+1/2=1$ das Ergebnis $1$ . Mit anderen Worten, das erste Bit im Zustand aus Gl. 3.15 ist deterministisch, die Wahrscheinlichkeiten beschreiben also nur das zweite Bit. Du kannst dir diesen Zustand also als “Kombination” der beiden getrennten Zustände $[1]$ und $\frac{1}{2}[0]+\frac{1}{2}[1]$ vorstellen (in Abschnitt 3.1.7 werden wir uns näher mit dem Kombinieren von probabilistischen Bits beschäftigen). Daher ist es nur logisch, dass das zweite Bit sich nach der Messung in einer Gleichverteilung befindet, also im Zustand

\frac{1}{2}[0]+\frac{1}{2}[1].

Im Allgemeinen starten wir mit zwei probabilistischen Bits in einem beliebigen Zustand

\displaystyle p_{00}[00]+p_{01}[01]+p_{10}[10]+p_{11}[11]

(3.16)

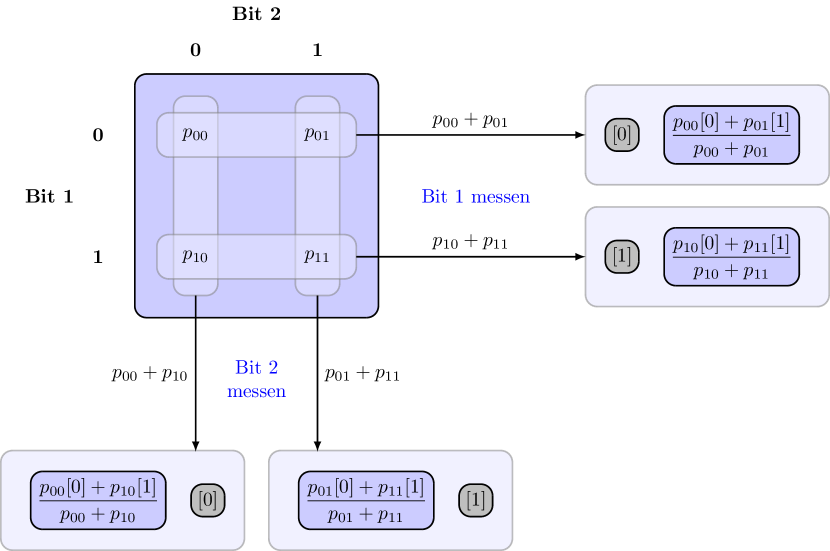
und messen das erste Bit. Dann wird der Zustand des anderen Bits vom Ergebnis der Messung abhängen. Wenn das Messergebnis beispielsweise $1$ war, betrachten wir wieder alle Terme aus Gl. 3.16, in denen das erste Bit den Zustand $1$ hat:

p_{10}[10]+p_{11}[11].

Dann ignorieren wir das erste Bit, da wir bereits wissen, dass es den Wert $1$ hat:

p_{10}[0]+p_{11}[1].

Und schließlich, da die Summe dieser Wahrscheinlichkeiten nicht zwingend $1$ ergibt, teilen wir sie durch ihre Summe $p_{10}+p_{11}$ :

\frac{p_{10}}{p_{10}+p_{11}}[0]+\frac{p_{11}}{p_{10}+p_{11}}[1].

(3.17)

Das ist die Wahrscheinlichkeitsverteilung des zweiten Bits, wenn die Messung des ersten Bits $1$ ergeben hat (siehe rechts in Abb. 3.3). Die übrigen Fälle sind auch in Abb. 3.3 zusammengefasst.

Refer to caption — Abbildung 3.3: Wahrscheinlichkeiten der Ergebnisse und die korrespondierenden Zustände des übrigen Bits, nachdem eines von zwei probabilistischen Bits gemessen wurde. Nach der Messung ist das gemessene Bit deterministisch (grau) während das andere probabilistisch bleibt (hellblau).

Um diese Regeln besser zu verstehen, zeigen wir, dass es keinen Unterschied macht, ob man beide Bits gleichzeitig misst oder zunächst das eine und anschließend das andere. So sollte die Wahrscheinlichkeit, $1$ vom ersten Bit und $0$ vom zweiten Bit zu erhalten einfach $p_{10}$ sein. Tatsächlich erhalten wir das Ergebnis $1$ beim messen des ersten Bits laut Gl. 3.14 mit Wahrscheinlichkeit $p_{10}+p_{11}$ und mit diesem Ergebnis muss laut Gl. 3.17 die Messung des zweiten Bits $0$ mit Wahrscheinlichkeit $p_{10}/(p_{10}+p_{11})$ ergeben. Damit ist die Gesamtwahrscheinlichkeit für den Fall, dass wir zunächst $1$ vom ersten und anschließend $0$ vom zweiten Bit erhalten

\displaystyle\left(p_{10}+p_{11}\right)\times\frac{p_{10}}{p_{10}+p_{11}}=p_{1% 0},

was genau dem erwarteten Ergebnis aus Gl. 3.4 entspricht. Die anderen Fälle können analog überprüft werden.

Übungsaufgabe 3.2 (Alice’ Münze erraten).

Problem: Alice ist im Besitz von drei Münzen $u,q,r$ mit den folgenden Verteilungen:

\displaystyle u=\begin{pmatrix}1/2\\ 1/2\end{pmatrix},

\displaystyle q=\begin{pmatrix}3/4\\ 1/4\end{pmatrix},

\displaystyle r=\begin{pmatrix}1/3\\ 2/3\end{pmatrix}.

Sie führt nun die folgende Sequenz von Würfen durch:

1.

Sie wirft die Münze $u$ .
2.
Je nach Ergebnis wirft sie eine der anderen beiden Münzen:
1. (0)
  
  wenn $u$ das Ergebnis $0$ hatte, wirft sie $q$ ;
2. (1)
  
  wenn $u$ das Ergebnis $1$ hatte, wirft sie $r$ .
3.

Alice erzählt Bob das Ergebnis ( $0$ oder $1$ ) des zweiten Münzwurfs (aber nicht, ob es das Ergebnis von $q$ oder $r$ ist).

Diese Situation besteht aus zwei probabilistischen Bits: Alice’ erster Münzwurf und Alice’ zweiter Münzwurf (der auch Bob’s probabilistischem Bit entspricht).

Fragen:

1.

Was ist die Wahrscheinlichkeitsverteilung der beiden Würfe von Alice?
2.

Was ist die Verteilung, wenn Bob sein probabilistisches Bit misst?
3.

Wenn Bob sein Bit misst und als Ergebnis $0$ erhält, ist es dann wahrscheinlicher, dass erste Münze $0$ oder $1$ war? Was wenn er $1$ misst?

Lösung.

1.

Wir bezeichnen mit $p$ die Wahrscheinlichkeitsverteilung von Alices zwei Münzwürfen. Wir benutzen Abb. 3.3 um die Wahrscheinlichkeiten zu bestimmen. Wir wissen, dass der erste Münzwurf von Alice verteilt ist nach $u$ , was bedeutet, dass wenn wir das erste Bit messen, wir jedes Bit mit Wahrscheinlichkeit je $1/2$ erhalten sollten:

$\displaystyle p_{00}+p_{01}=\frac{1}{2},\quad p_{10}+p_{11}=\frac{1}{2}.$

Wenn der erste Münzwurf eine $0$ ergab, dass sollte der Zustand des zweiten Bits beschrieben werten durch die Münze $q$ . D.h., wir müssen haben:

$\displaystyle\frac{p_{00}[0]+p_{01}[1]}{p_{00}+p_{01}}=\frac{3}{4}[0]+\frac{1}% {4}[1],$

Davon können wir ableiten, dass $p_{00}=\frac{3}{8}$ and $p_{01}=\frac{1}{8}$ . Analog dazu gilt: Wenn der erste Münzwurf eine $1$ war, dann wird der Zustand des zweiten Bits beschrieben durch die Münze $r$ , also

$\displaystyle\frac{p_{10}[0]+p_{11}[1]}{p_{00}+p_{01}}=\frac{1}{3}[0]+\frac{2}% {3}[1],$

ergo $p_{10}=\frac{1}{6}$ and $p_{11}=\frac{2}{6}$ . Zusammen gilt:

$\displaystyle p=\frac{3}{8}[00]+\frac{1}{8}[01]+\frac{1}{6}[10]+\frac{2}{6}[11],$
2.

Der Wert von Bob’s Bit ist der Gleiche wie das Ergebnis von Alices zweitem Münzwurf, also folgen wir einfach Abb. 3.3 um die Wahrscheinlichkeit der Ergebnisse zu bestimmen, wenn wir das zweite Bit messen. Die Wahrscheinlichkeit, dass Bobs Ausgabe $0$ ist, ist also

$\displaystyle p_{00}+p_{10}=\frac{3}{8}+\frac{1}{6}=\frac{13}{24}$

und die Wahrscheinlichkeit, dass seine Ausgabe $1$ ist, ist $1-\frac{13}{24}=\frac{11}{24}$ . Wir können dies durch die folgende Zufallsverteilung beschreiben:

$\displaystyle\frac{13}{24}[0]+\frac{11}{24}[1].$
3.

Wir benutzen wieder Abb. 3.3. Wenn das zweite Bit gemessen wird und das Ergebnis $0$ ist, dann ist der Zustand des ersten Bits gegeben durch

$\displaystyle\frac{p_{00}[0]+p_{10}[1]}{p_{00}+p_{10}}=\frac{9}{13}[0]+\frac{4% }{13}[1].$

Es ist also wahrscheinlicher, dass Alices erster Münzwurf das Ergebnis $0$ zeigt.

Analog dazu, wenn das Ergebnis vom Messen des zweiten Bits $1$ ist, dann wird der Zustand des erstens Bits beschrieben durch

$\displaystyle\frac{p_{01}[0]+p_{11}[1]}{p_{01}+p_{11}}=\frac{3}{11}[0]+\frac{8% }{11}[1].$

In diesem Fall ist es wahrscheinlicher, dass Alices erster Münzwurf $1$ ist.