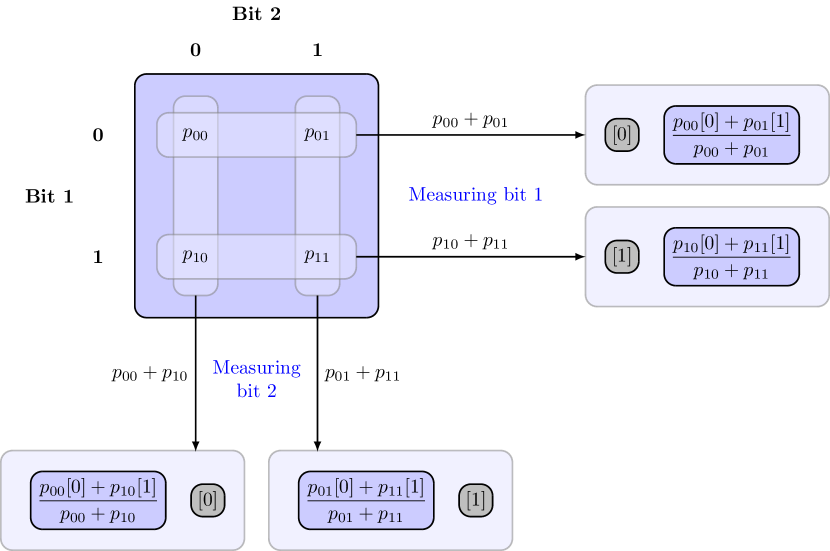
3.1.4 State of the other bit

After the measurement, the bit that was measured is in a deterministic state that corresponds to the measurement outcome (just as when measuring a single bit – see Eq. 1.32). But how about the other bit that was not measured? Its state after the measurement in general will not be deterministic. For example, if the initial state of the two probabilistic bits is

\frac{1}{2}[10]+\frac{1}{2}[11]

(3.15)

and the first bit is measured, the probability of observing $1$ is $1/2+1/2=1$ . In other words, the first bit in Eq. 3.15 is deterministic and the two probabilities actually describe only the second bit. Hence, you can intuitively think of this state as the result of “combining” together two separate probabilistic bits: $[1]$ and $\frac{1}{2}[0]+\frac{1}{2}[1]$ (we will talk more about how to combine two probabilistic bits in Section 3.1.7). Therefore it makes sense that the state of the second bit after the measurement should be uniformly random, namely

\frac{1}{2}[0]+\frac{1}{2}[1].

More generally, suppose that we start with two probabilistic bits in an arbitrary state

\displaystyle p_{00}[00]+p_{01}[01]+p_{10}[10]+p_{11}[11]

(3.16)

and measure the first bit. The state of the remaining bit will generally depend on the measurement outcome. For example, if the outcome was $1$ , to find the state of the second bit we first collect all terms in Eq. 3.16 where the first bit has value $1$ :

p_{10}[10]+p_{11}[11].

Then, we ignore the first bit since we already know that its value is $1$ :

p_{10}[0]+p_{11}[1].

Finally, since these two probabilities may not sum to one, we divide them by their sum $p_{10}+p_{11}$ :

\frac{p_{10}}{p_{10}+p_{11}}[0]+\frac{p_{11}}{p_{10}+p_{11}}[1].

(3.17)

This is the probability distribution on the second bit when the first bit is measured and yields outcome $1$ (see the right side of Fig. 3.3). The remaining cases are also summarized in Fig. 3.3.

Refer to caption — Figure 3.3: Outcome probabilities and the state of the remaining bit when measuring one out of two probabilistic bits. After the measurement, the bit that was measured becomes deterministic (gray) while the other bit stays probabilistic (light blue).

To see that these rules make sense, let us verify that measuring the first bit and then the second bit gives the same probabilities as directly measuring both bits. For example, the probability of obtaining $1$ from the first bit and $0$ from the second bit should simply be $p_{10}$ . Indeed, according to Eq. 3.14, we obtain the outcome $1$ from the first bit with probability $p_{10}+p_{11}$ and, given this outcome, Eq. 3.17 asserts that we obtain the outcome $0$ from the second bit with probability $p_{10}/(p_{10}+p_{11})$ . Thus the total probability of first obtaining $1$ from the first bit and then $0$ from the second bit is

\displaystyle\left(p_{10}+p_{11}\right)\times\frac{p_{10}}{p_{10}+p_{11}}=p_{1% 0},

which is exactly what we want according to Eq. 3.4. The other cases can be verified similarly.

Exercise 3.2 (Guessing Alice’s coin).

Problem: Alice has three coins called $u$ , $q$ , $r$ with the following probability distributions:

\displaystyle u=\begin{pmatrix}1/2\\ 1/2\end{pmatrix},

\displaystyle q=\begin{pmatrix}3/4\\ 1/4\end{pmatrix},

\displaystyle r=\begin{pmatrix}1/3\\ 2/3\end{pmatrix}.

Alice performs the following sequence of coin tosses:

1.

She tosses the coin $u$ .
2.
Depending on the outcome, she tosses one of the other two coins:
1. (0)
  
  if $u$ produced $0$ , she tosses $q$ ;
2. (1)
  
  if $u$ produced $1$ , she tosses $r$ .
3.

Alice tells her friend Bob the outcome ( $0$ or $1$ ) of the coin she tossed in step 2 (but she does not tell whether it was produced by tossing the coin $q$ or $r$ ).

In this situation there are two probabilistic bits: Alice’ first coin toss and Alice’ second coin toss (which is exactly the same as Bob’s probabilistic bit).

Questions:

1.

What is the probability distribution of Alice’ two coin tosses?
2.

What is the probability distribution when Bob measures his probabilistic bit?
3.

Given that Bob measures his bit and obtains outcome $0$ , is it more likely that Alice’ first coin shows $0$ or $1$ ? How about if his outcome is $1$ ?

Solution.

1.

Let us denote the probability distributions of Alice‘ two coin flips by $p$ . We use Fig. 3.3 to figure out the probabilities. We know that Alice first coin flip is distributed according to $u$ , which means that if we measure the first bit then we should get both outcomes with probability $1/2$ :

$\displaystyle p_{00}+p_{01}=\frac{1}{2},\quad p_{10}+p_{11}=\frac{1}{2}.$

Next, we know that if the first coin flip gave outcome $0$ then the state of the second bit should be described by the coin $q$ . Thus we must have

$\displaystyle\frac{p_{00}[0]+p_{01}[1]}{p_{00}+p_{01}}=\frac{3}{4}[0]+\frac{1}% {4}[1],$

from which we deduce that $p_{00}=\frac{3}{8}$ and $p_{01}=\frac{1}{8}$ . Similarly, if the first coin flip gave outcome $1$ then the state of the second bit is described by coin $r$ , so

$\displaystyle\frac{p_{10}[0]+p_{11}[1]}{p_{00}+p_{01}}=\frac{1}{3}[0]+\frac{2}% {3}[1],$

hence $p_{10}=\frac{1}{6}$ and $p_{11}=\frac{2}{6}$ . Together,

$\displaystyle p=\frac{3}{8}[00]+\frac{1}{8}[01]+\frac{1}{6}[10]+\frac{2}{6}[11],$
2.

The value of Bob’s bit is the same as the outcome of Alice’ second coin flip, so we simply follow Fig. 3.3 to compute the probability of outcomes when measuring the second bit. Thus, the probability that Bob’s outcome is $0$ is

$\displaystyle p_{00}+p_{10}=\frac{3}{8}+\frac{1}{6}=\frac{13}{24}$

and the probability that his outcome is $1$ is $1-\frac{13}{24}=\frac{11}{24}$ . We can write this as the probability distribution

$\displaystyle\frac{13}{24}[0]+\frac{11}{24}[1].$
3.

Again we use Fig. 3.3. If the second bit is measured and the result is outcome $0$ then the state of the first bit is given by

$\displaystyle\frac{p_{00}[0]+p_{10}[1]}{p_{00}+p_{10}}=\frac{9}{13}[0]+\frac{4% }{13}[1].$

Thus it is more likely that Alice’ first coin flip shows $0$ .

Similarly, if the result of measuring the second bit is $1$ then the state of the first bit is described by

$\displaystyle\frac{p_{01}[0]+p_{11}[1]}{p_{01}+p_{11}}=\frac{3}{11}[0]+\frac{8% }{11}[1].$

In this case, it is more likely that Alice’ first coin flip shows $1$ .