3.1.3 Measuring only one bit

If you have two probabilistic bits and you measure only one of them, what are the probabilities to get each of the two outcomes? Our notation is particularly convenient for figuring this out. Consider again a general probabilistic two-bit state

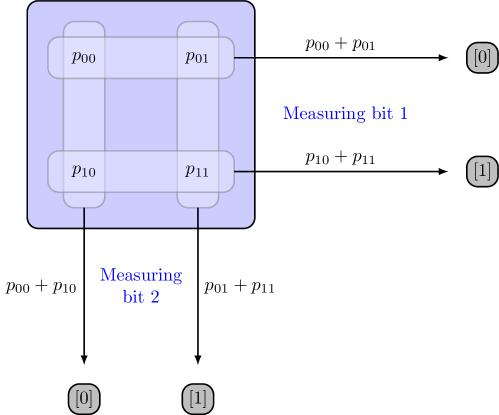
To find the probability of outcome $0$ when measuring some bit, you simply sum together the probabilities of all terms where the bit you are measuring is in the desired state $0$; similarly for the outcome $1$.

For example, the probability of observing outcome $1$ when measuring the first bit is

corresponding to the probabilities in Eq. 3.4 that lead to $[10]$ and $[11]$, which are the two bit strings that start with $1$. Similarly, the probability of observing outcome $0$ when measuring the second bit is

corresponding to the probabilities that lead to the two bit strings that end with zero, $[00]$ and $[10]$. It is easy to compute this if you arrange the four probabilities in a $2\times 2$ square, as in Fig. 3.2.

We can also use Quirky to display the probabilities when measuring a single bit. Simply resize the probability display so that it only covers a single wire, like so:

In fact, we can view both the probabilities of outcomes when measuring only the first bit and the probabilities of outcomes when measuring only the second bit at the same time:

Note that the result is very intuitive. Since the two bits are never “correlated”, it is clear that the first bit should be in state $\frac{1}{3}[0]+\frac{2}{3}[1]$ and the second bit in state $[1]$.